Se dice que una vez a Albert Einstein le preguntaron cual era la fuerza más poderosa del Universo, a lo cual respondió: el interés compuesto.
Sea real o no esa afirmación, describiremos a grandes rasgos en que consiste el interés compuesto y como aplicarlo a tus finanzas.
El interés compuesto, es simplemente una suma de valores que no son lineales, sino que en cada nueva suma, se agrega un porcentaje de variación, la cual si es positiva en el largo plazo, en vez de entregar un aumento lineal, entrega un aumento exponencial.
Ésta fórmula se puede utilizar para muchos parámetros en las matemáticas y física, pero en este blog lo aplicaremos al interés obtenido de rendimientos de inversión de dinero. La fórmula es la siguiente:
M = C (1 + i)n
Donde:
- M es la suma de capital más intereses al final del ciclo.
- C es el capital inicial.
- i es la tasa de interés compuesto.
- n es el número de ciclos durante los cuales se capitaliza el interés compuesto.
Esto se aplica en la reinversión de las ganancias o rendimientos. Dejaré un ejemplo para entender.
Supongamos que tengo un negocio o inversión que genera un 10% de rendimiento del dinero invertido en cada ciclo. Está la opción de retirar ese 10% y gastarlo conservando el capital, o ese 10% volverlo a invertir en el siguiente ciclo. El resultado de hacer ambas operaciones es el siguiente (iniciaremos con 100 dólares, sin otras inyecciones de capital):
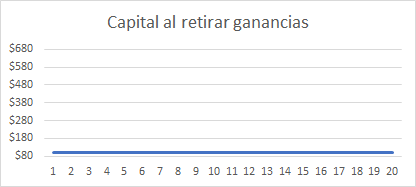
Caso 1: Retirar el rendimiento:
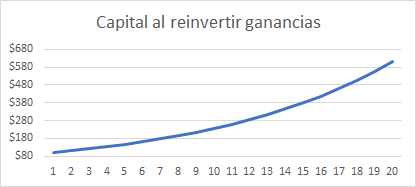
Caso 2: Reinvertir el rendimiento:
En un periodo de 20 ciclos, se observa que al momento de retirar el rendimiento, se obtienen 10 dólares cada vez, y se mantiene el capital invertido de 100 dólares constante. La ganancia retirada fue de 200 dólares. En caso de que al final del periodo total, se quiera retirar el capital, el total retirado es de 300 dólares (100 de capital + 200 de ganancias). Se observa una recta constante del capital en el gráfico.
Mientras que al reinvertir el capital en vez de retirarlo, en el mismo fin los 20 ciclos, el monto final del periodo en caso de que se quiera retirar es de 673 dólares (612 de capital + 61 del último rendimiento). Lo cual es más del doble. pero lo interesante es que se vuelve exponencial, y entre más periodos se pueden observar mejores resultados.
Suponiendo el mismo ejemplo, en 100 ciclos, los resultados son los siguientes:
- En caso de retiro de rendimientos: Se finaliza con 1.100 dólares (100 de capital + 1.000 de retiros).
- En caso de reinversión de rendimientos: Se finaliza con 1.378.061 dólares (1.252.783 de capital + 125.278 del último rendimiento). La diferencia es enorme, más de 1.250 veces el primer caso.
Esto también se puede plasmar en caso de que vayamos agregando 100 dólares en cada ciclo.
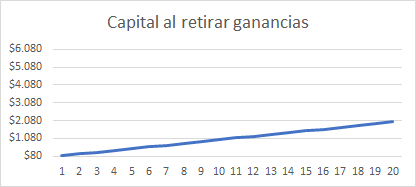
Sin interés compuesto los resultados serían los siguientes:
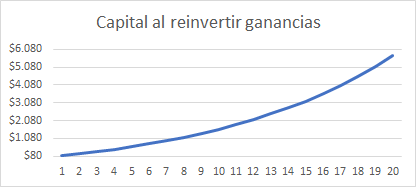
Con interés compuesto los resultados serían los siguientes:
En 20 ciclos los resultados finales son:
- En caso de retiro de rendimientos: Se aportan 2.000 dólares de capital y se finaliza con 4.100 dólares (los 2.000 de capital + 2.100 de retiros).
- En caso de reinversión de rendimientos: Se aportan 2.000 dólares de capital y se finaliza con 6.300 dólares (5.727 de capital con rendimientos + 573 del último rendimiento). La diferencia no es tan amplia, ya que son los ciclos iniciales, donde el capital inyectado si tiene un factor determinante.
Mientras que en 100 ciclos los resultados finales son:
- En caso de retiro de rendimientos: Se aportan 10.000 dólares de capital y se finaliza con 60.500 dólares (10.000 de capital + 50.500 de retiros).
- En caso de reinversión de rendimientos: Se aportan 10.000 dólares de capital y se finaliza con 15.157.574 dólares (13.779.612 de capital con rendimientos + 1.377.961 del último rendimiento).
Por lo mismo, utilizando estas herramientas, puedes planificar negocios o inversiones para obtener los resultados que tengas como objetivo, y ver si para ti es más importante la satisfacción inmediata al retirar los dineros en cada ciclo, o la recompensa a la paciencia y disciplina al pargo plazo, hasta que sea lo suficientemente grande como para que puedas hacer retiros de rendimientos sin que se afecte significativamente tu capital. Es decir, vivir de tus inversiones. o ser libre financieramente.







5 respuestas
[…] que es un plan a largo plazo. Entre antes uno empiece es mejor, sobre todo si se aplica el interés compuesto, que explicamos en una entrada […]
[…] de la regla del 4% para la libertad financiera, explicada en una entrada anterior. Y aprovechar el interés compuesto, con el cual entre antes empieces, mejor lo puedes […]
[…] hemos planteado en el interés compuesto, la fuerza más poderosa, lo cual también se puede aplicar a negocios, entre antes comiences siempre va a ser mejor, ya que […]
[…] plazo y los resultados a corto plazo son mínimos o nulos. Esto lo podemos ejemplificar al aplicar el interés compuesto, donde los resultados se vuelven exponenciales, pero el tiempo es un factor fundamental para […]
[…] Si esta resta genera un resultado positivo, generalmente se le llama ahorro, el cual si es bien utilizado se hace crecer, al comprar activos que generen cashflow, aumento de patrimonio y ganancias de capital. Y esto a su vez va generando más ingresos, repitiendo la fórmula una y otra vez volviéndola exponencial. Este es el fundamento base del interés compuesto. […]